 알고리즘) Disjoint-set Algorithm (서로소 집합 알고리즘)
알고리즘) Disjoint-set Algorithm (서로소 집합 알고리즘)
Disjoint-set Algorithm (서로소 집합 알고리즘) 집합, 그룹을 관리하는 알고리즘 각 그룹을 트리구조로 관리 크게 2가지의 연산으로 구성된다. find(x) : x번 노드의 root를 찾는 함수 link(x, y) : x 노드가 속한 그룹과 y 노드가 속한 그룹을 합치는(연결하는) 함수 또한 위 연산을 위해, parent[i] : i번 노드의 부모로 정의되는 배열이 사용된다. 아래의 내용은 codeground 사이트에서 가져온 내용 Disjoint-Set 서로소 집합(Disjoint-Set)은 집합, 혹은 그룹을 관리하는 효율적인 알고리즘입니다. 각각의 그룹을 트리 구조로 관리하는 이 알고리즘은 크게 두 가지의 연산을 가집니다. find(x): x번 노드의 최고 조상(루트)을 찾는 함수 ..
 알고리즘) Graph - Dijkstra/Floyd-Warshall/Bellman-Ford 's Alg (distance)
알고리즘) Graph - Dijkstra/Floyd-Warshall/Bellman-Ford 's Alg (distance)
Dijkstra Algorithm 그래프의 한 노드에서 다른 노드로 가는 최단거리를 구하는 알고리즘 (만약 모든 노드 쌍간의 최단거리를 구할땐, n개의 각 정점에 대해 Dijkstra Alg를 여러번 수행해야하므로, 이때는 Floyd-Warshall Alg이 더 유리하다) 동작과정은 BFS와 비슷하지만, Queue가 아닌 Priority Queue를 이용한다. 시간복잡도=O(ElogE) 해당노드까지의 최단거리를 저장할 distance[] 배열 준비후, 미방문을 의미하는 -1로 초기화한다. 노드1에서 시작한다면, 이때까지 자기자신 1까지의 거리는 0이므로 distance[1]에 0을, pq에 (1,0)을 넣는다. 2의10보다 가깝다. distance[2]=8로 갱신, pq에도 (2,8) 넣는다. pq엔 (..
 알고리즘) Graph - MST (Minimum_Cost Spanning Tree) using Prim/Kruskal's Algorithm
알고리즘) Graph - MST (Minimum_Cost Spanning Tree) using Prim/Kruskal's Algorithm
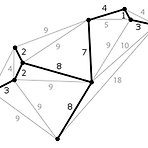
MST,MCST (Minimun_Cost Spanning Tree) (최소비용 신장트리) Spanning Tree : undirected graph에서 n개의 모든정점과 n-1개의 간선으로 만들어진 트리 순회(traversal)를 하면 n-1개의 간선을 이동하며 모든 정점을 방문하므로 spanning tree를 생성한다. DFS로 생성되면 DFST(Depth First Spanning Tree, 깊이우선 신장트리), BFS로 생성되면 BFST(Breadth First Spanning Tree, 너비우선 신장트리)라고 한다. weighted undirected graph에서 모든 노드를 포함하고 cycle이 없으며 weight의 합이 최소인 트리를 MST or MCST(Minimum Cost Spannin..
 알고리즘) Graph - DFS, BFS (깊이우선탐색, 너비우선탐색)
알고리즘) Graph - DFS, BFS (깊이우선탐색, 너비우선탐색)
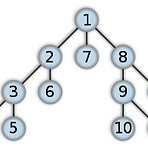
DFS (Depth First Search) (깊이 우선 탐색) LIFO(Last-In First-Out), Stack 활용 PseudoCode recursive non-recursive 1 non-recursive 2 예제 Input Output 첫 줄에 정점의 개수 N과 간선의 개수 M이 주어집니다. 다음 M줄에 간선의 관계 시작정점 u와 도착정점 v가 주어집니다. 입력에 따른 깊이 우선 탐색 결과를 출력합니다. import java.util.*; public class Test { static boolean edge[][]; static boolean visited[]; static int n; static int m; public static void main(String args[]) { Sca..
 자료구조) Graph (그래프)
자료구조) Graph (그래프)
Graph (그래프) Traversal / Search (순회,탐색) DFS(Depth First Search) 깊이우선탐색 BFS(Breadth First Search) 너비우선탐색 Spanning Tree (신장트리) DFST(Depth First Spanning Tree) 깊이우선 신장트리 BFST(Breadth First Spanning Tree) 너비우선 신장트리 MST,MCST(Minimum_Cost Spanning Tree) 최소_비용 신장트리 : Kruskal, Prim 's Alg Distance (최단거리 등) Dijkstra 's Alg Floyd-Warshall 's Alg Bellman-Ford 's Alg Etc Network Flow Bipartit..
 자료구조) Tree - Binary Search Tree, Segment Tree, Binary Indexed Tree
자료구조) Tree - Binary Search Tree, Segment Tree, Binary Indexed Tree
Binary Search Tree (이진 탐색 트리) def 모든 원소는 서로다른 유일한 값. 왼쪽 subtree의 값은 그 root보다 작다. 오른쪽 subtree의 값은 그 root보다 크다. 왼/오른쪽 subtree도 Binary Search Tree이다. 탐색/삽입/삭제 중 삭제연산이 번거롭다. 노드를 삭제한 후에도 BST를 유지해야하므로 후속조치가 필요하다. 삭제할 노드가 1. degree=0(leaf node)인지 2. degree=1인지 3. degree=2인지에 따라 달라짐. Segment Tree 구간의 정보를 빠르게 구할수있는, Complete Binary Tree 형태의 자료구조 Example) 구간 최소값을 구하는 Segment Tree 구하려는 데이터 배열을 완전이진트리의 최하단에..
 자료구조) Tree - Heap, Priority Queue (힙, 우선순위 큐)
자료구조) Tree - Heap, Priority Queue (힙, 우선순위 큐)
Heap (힙) Max Heap / Min Heap Parent Node가 Child Node보다 항상 크거나(작거나) 같은 Complete Binary Tree (완전이진트리) (자식노드끼리는 상관없음) (항상 root가 max/min이므로 최대-최소값을 찾기 편하다) 시간 복잡도 : O(logn) (힙의 삽입-삭제는 최악의 경우, 최하단노드~최상단노드까지 swap이 필요하다) 삽입&삭제 시에도 '완전이진트리'형태를 유지해야한다. 삽입 : 마지막 노드의 다음자리를 확장하고 임시로 저장후, 부모노드와 비교해가며 swap한다. 삭제 : 항상 root를 삭제해 반환한다. 마지막 노드를 root자리에 임시로 저장후 삭제하고, root에 있는 값을 자식들과 비교해가며 적당한 자리까지 swap한다...
 자료구조) Tree, Binary Tree (트리, 이진트리)
자료구조) Tree, Binary Tree (트리, 이진트리)
Tree 용어 : Root, Child, Parent, Siblings, Leaf=Terminal, Branch=Internal, Degree, Height, Level => 모든 노드의 Degree(차수)가 2이하 Binary Tree 구현 순차 자료구조 (ex. 배열) Node (of Node i)IndexConditionParentfloor( i/2 )i > 1Left Child2i2i ≤ nRight Child2i+1(2i+1) ≤ nRoot10 < n 연결 자료구조 (ex. 하단 코드) class TreeNode { Object data; TreeNode left; TreeNode right; }Traversal (순회) : Pre-order, In-order, Post-order D L R (..
- Total
- Today
- Yesterday
- 해외여행
- 리버싱
- Vo
- Android Studio
- queue
- git
- dfs
- 웹해킹
- bfs
- C
- OneToMany
- webhacking.kr
- 우아한 테크코스
- JPA
- FRAGMENT
- graph
- Algorithm
- reversing
- mysql
- javascript
- 회고
- Stack
- Java
- Android
- brute-force
- socket
- sort
- Data Structure
- 개발자
- 프로그래머스
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
