티스토리 뷰
알고리즘) Graph - MST (Minimum_Cost Spanning Tree) using Prim/Kruskal's Algorithm
os94 2019. 9. 13. 13:56MST,MCST (Minimun_Cost Spanning Tree) (최소비용 신장트리)
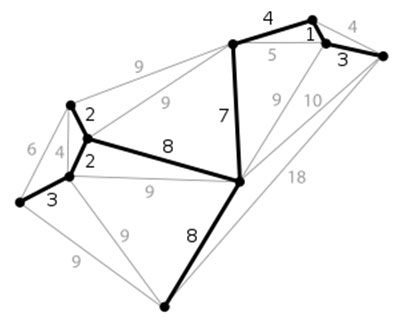
Spanning Tree : undirected graph에서 n개의 모든정점과 n-1개의 간선으로 만들어진 트리
순회(traversal)를 하면 n-1개의 간선을 이동하며 모든 정점을 방문하므로 spanning tree를 생성한다.
DFS로 생성되면 DFST(Depth First Spanning Tree, 깊이우선 신장트리), BFS로 생성되면 BFST(Breadth First Spanning Tree, 너비우선 신장트리)라고 한다.
weighted undirected graph에서 모든 노드를 포함하고 cycle이 없으며 weight의 합이 최소인 트리를 MST or MCST(Minimum Cost Spanning Tree, 최소비용 신장트리)라고 한다.
MST를 만드는데 주로 Prim or Kruskal 's Alg를 사용한다.
Prim's Algorithm in MST
- 아무 정점으로 시작점을 정한다.
- 연결된 모든 간선들 중에서 weight가 가장 작은 간선을 선택해 연결한다.
- 선택된 정점들과 연결된 모든 간선들 중에서 weight가 가장 작은 간선을 선택해 연결한다. (반복)
이때 물론, cycle을 형성하는 것은 선택할수없다. 그 다음것 선택. - 간선이 n-1개가 되면 MST 완성.

인접행렬로 구현시 시간복잡도=O(V2)
이진힙,우선순위큐로 구현시 시간복잡도=O(ElogV)
예제
|
Input |
Output |
|
첫째 줄에 정점의 수 자연수 n과 간선의 수 자연수 m이 주어진다. 두 번째 줄 ~ m + 1번째 줄까지는 간선의 정보인 정수 X, Y, COST가 차례로 주어진다. 이는 X와 Y를 잇는 가중치가 COST인 간선이 존재한다는 의미이다. |
MST를 만드는 최소비용을 출력한다. |
import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.Scanner;
class Node implements Comparable<Node> {
int x, y;
public Node() {}
public Node(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(Node arg0) { // pq안에 들어가서 노드끼리 비교하게될때 y값=weight가 작을수록 큰 우선순위를 갖게함
return this.y - arg0.y;
}
}
public class Test {
int visited[]; // visited[?]==1이면 정점?는 방문,선택되었다는것
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // # of V
int m = sc.nextInt(); // # of E
ArrayList<Node> g[] = new ArrayList[10005]; // g라는 ArrayList 각각 안에 ArrayList가 담긴다
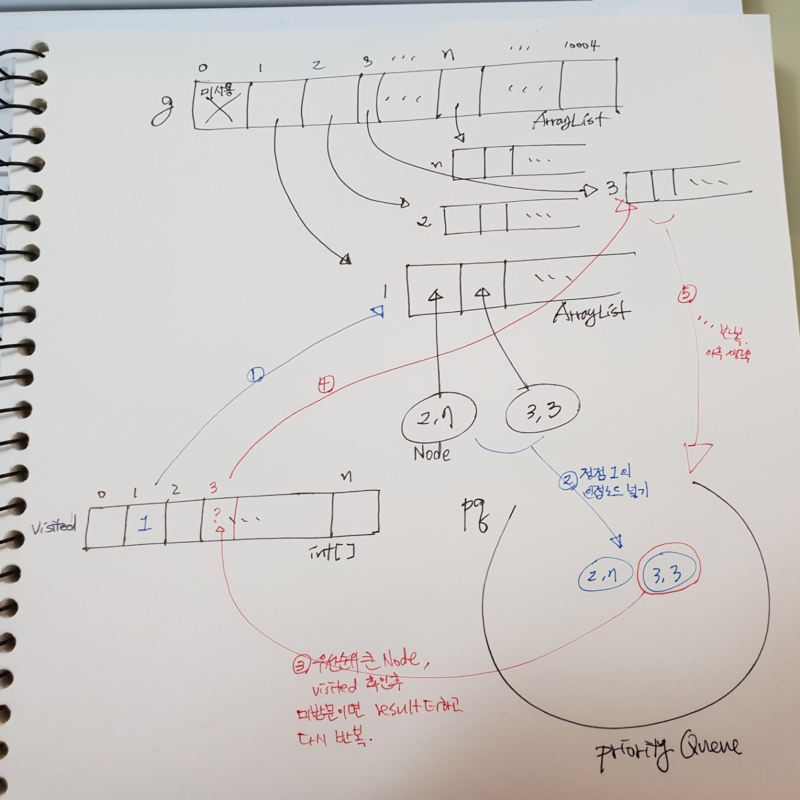
PriorityQueue<Node> pq = new PriorityQueue<Node>(); // pq는 선택된 모든정점들과 연결된 간선들 pool
for (int i = 1; i <= n; i++)
g[i] = new ArrayList<>();
for (int i = 0; i < m; i++) {
int x = sc.nextInt();
int y = sc.nextInt();
int z = sc.nextInt();
g[x].add(new Node(y, z));
g[y].add(new Node(x, z));
}
int selected = 1, result = 0; // start vertex = 1로 시작. result is sum of weight
int visited[] = new int[n + 1];
for (int i = 0; i < n - 1; i++) {
visited[selected] = 1; // 해당 정점 방문 표시
for (int j = 0; j < g[selected].size(); j++) {
pq.add(g[selected].get(j)); // g[selected].get(j) is Node(?,?). pq풀에 selected정점과 연결된 간선들 모두 집어넣는다
}
while (visited[pq.element().x] == 1) { // pq.element().x is 도착정점. visited[?]==1은 이미 방문한 노드임을 의미, 이미 방문했으므로 패스하는 루틴
pq.remove(); // remove()의 인자가없으므로 우선순위가 가장높은것을 삭제(하고 반환)
}
result += pq.element().y; // add weight to result
selected = pq.peek().x; // remove와 달리 우선순위가 가장높은것을 삭제하진않고 반환만 한뒤, 그것의 x값을 s에 넣는다. 즉 selected에 선택한 정점이 담긴다.
pq.remove(); // 바로 윗줄에서 선택했으니 이제 그건 풀에서 제거
}
System.out.println(result);
}
}
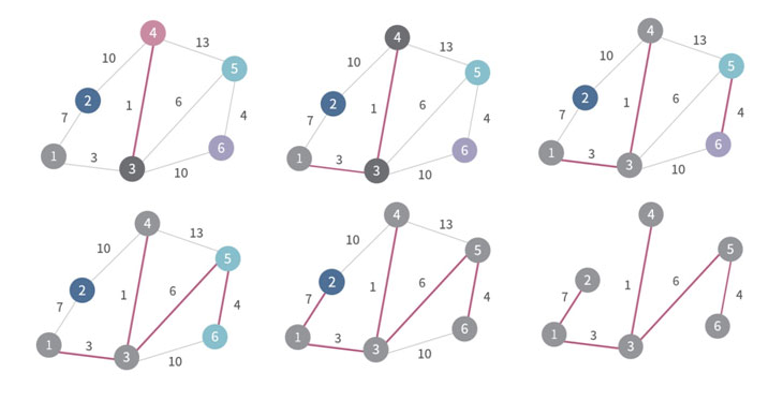
Kruskal Algorithm : 1. weight가 높은 간선을 제거 2. weight가 낮은 간선을 삽입
Kruskal's Algorithm 1 in MST
- 모든 간선을 weight로 내림차순 정렬한다.
- weight가 가장 높은 간선부터 차례대로 제거한다. (반복)
이때 물론, 정점을 분리시키는 것은 선택할수없다. 그 다음것 선택. - n-1개의 간선만 남으면 MST 완성.
Kruskal's Algorithm 2 in MST
- 모든 간선을 weight로 오름차순 정렬한다.
- weight가 가장 낮은 간선부터 차례대로 삽입한다. (반복)
이때 물론, cycle을 형성하는 것은 선택할수없다. 그 다음것 선택. (Disjoint-set Alg을 이용해 두 정점이 같은그룹인지 확인, 다른그룹이라면 두 정점을 연결하고 병합과정을 통해 같은그룹으로 합침 _별도포스팅참고) - n-1개의 간선이 되면 MST 완성.
예제
|
Input |
Output |
|
첫째 줄에 정점의 수 자연수 n과 간선의 수 자연수 m이 주어진다. 두 번째 줄 ~ m + 1번째 줄까지는 간선의 정보인 정수 X, Y, COST가 차례로 주어진다. 이는 X와 Y를 잇는 가중치가 COST인 간선이 존재한다는 의미이다. |
MST를 만드는 최소비용을 출력한다. |
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
class Node implements Comparable<Node> {
int x, y, z;
public Node() {}
public Node(int x, int y, int z) {
this.x = x;
this.y = y;
this.z = z;
}
@Override
public int compareTo(Node arg0) {
return this.z - arg0.z;
}
}
public class Test {
static int uf[];
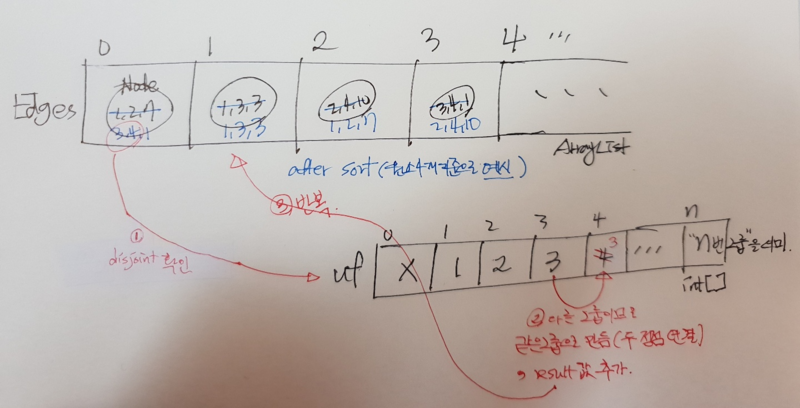
static int disjoint(int x) { // 다른 그룹인지, 즉 연결하면 cycle이 형성되지않는지 판별해주는 함수. 자세한 disjoint-set Alg는 별도 참조
if(x != uf[x])
return uf[x] = disjoint(uf[x]);
else
return x;
}
public static void main(String[] args) {
ArrayList<Node> Edges = new ArrayList<Node>(); // 간선 집합. 추후 sort()를 이용해 오름차순으로 정렬됨
Scanner sc = new Scanner(System.in);
int v = sc.nextInt(); // # of V
int e = sc.nextInt(); // # of E
uf = new int[v + 1]; // 각 정점이 담고있는 원소에 대한 정보 제공. 두 정점이 이어져서 연결되면 같은 그룹이 되어 같은 데이터를 담게된다
for (int i = 1; i <= v; i++) // 초기화
uf[i] = i;
for (int i = 0; i < e; i++)
Edges.add(new Node(sc.nextInt(), sc.nextInt(), sc.nextInt()));
Collections.sort(Edges); // 오름차순으로 간선 정렬
long result = 0;
for (int i = 0; i < e; i++) {
int x = Edges.get(i).x, y = Edges.get(i).y; // 두 정점 그대로 꺼내와서
if (disjoint(y) != disjoint(x)) { // 다른 그룹이면, 즉 두 정점이 같은 그룹이면 연결시 cycle이 형성되므로
uf[disjoint(y)] = uf[x]; // 두 정점 같은 그룹으로 만들어 연결시킴
result += Edges.get(i).z; // add weight to result
}
}
System.out.println(result);
}
}
'Algorithm' 카테고리의 다른 글
| 알고리즘) Disjoint-set Algorithm (서로소 집합 알고리즘) (0) | 2019.09.13 |
|---|---|
| 알고리즘) Graph - Dijkstra/Floyd-Warshall/Bellman-Ford 's Alg (distance) (0) | 2019.09.13 |
| 알고리즘) Graph - DFS, BFS (깊이우선탐색, 너비우선탐색) (0) | 2019.09.12 |
| 알고리즘) Two Pointer, Sliding Window (0) | 2019.09.12 |
| 알고리즘) Heap/Tree Sort (힙/트리 정렬) (0) | 2019.09.12 |
- Total
- Today
- Yesterday
- Algorithm
- C
- Stack
- brute-force
- Data Structure
- git
- sort
- Android
- 개발자
- Vo
- 회고
- 웹해킹
- graph
- JPA
- 리버싱
- dfs
- bfs
- Android Studio
- 해외여행
- OneToMany
- 프로그래머스
- socket
- webhacking.kr
- reversing
- queue
- FRAGMENT
- javascript
- 우아한 테크코스
- Java
- mysql
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
