티스토리 뷰
알고리즘) Graph - Dijkstra/Floyd-Warshall/Bellman-Ford 's Alg (distance)
os94 2019. 9. 13. 14:00Dijkstra Algorithm
그래프의 한 노드에서 다른 노드로 가는 최단거리를 구하는 알고리즘
(만약 모든 노드 쌍간의 최단거리를 구할땐, n개의 각 정점에 대해 Dijkstra Alg를 여러번 수행해야하므로, 이때는 Floyd-Warshall Alg이 더 유리하다)
- 동작과정은 BFS와 비슷하지만, Queue가 아닌 Priority Queue를 이용한다.
- 시간복잡도=O(ElogE)
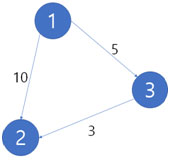
해당노드까지의 최단거리를 저장할 distance[] 배열 준비후, 미방문을 의미하는 -1로 초기화한다.
노드1에서 시작한다면, 이때까지 자기자신 1까지의 거리는 0이므로
distance[1]에 0을, pq에 (1,0)을 넣는다. <= (정점,거리) 의미
이후 BFS처럼 연결된 정점들을 확인한다.
pq에 (2,0+10), (3,0+5)을 넣고, distance[2]=10, distance[3]=5를 넣는다.
pq가 Min-Heap이라면 2번보다 3번을 먼저 방문한다.
3번 방문후 또 연결된 정점들을 확인한다.
2번 정점이 있는데 0+5+3=8이 기존 1->2의10보다 가깝다.
distance[2]=8로 갱신, pq에도 (2,8) 넣는다.
pq엔 (2,10), (2,8)만 남았고 역시 min-heap이므로 (2,8)를 꺼낸다.
해당 경로를 통해 2번 정점 방문후, 더이상 연결된 정점이 없으므로 (2,10)가 나온다.
distance[2]=8이 10보다 작으므로 continue로 넘어간다.
pq가 비었으므로 전체과정 종료.
|
Input |
Output |
|
첫 줄에 정점의 개수 N과 간선의 개수 M, 그리고 시작 정점 S가 주어집니다. 다음 M줄에 간선의 관계 시작정점 u와 도착정점 v 그리고 간선 가중치 w가 주어집니다. |
시작정점에서 각 정점사이의 거리를 모두 출력합니다. |
import java.util.*;
class Edge implements Comparable<Edge> {
int dst, weight;
public Edge(){}
public Edge(int dst, int weight) {
this.dst = dst;
this.weight = weight;
}
@Override
public int compareTo(Edge arg0) {
return this.weight - arg0.weight;
}
}
public class Test {
static Vector<Vector<Edge>> edge;
static int V;
static int E;
static int start;
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
V = scanner.nextInt();
E = scanner.nextInt();
start = scanner.nextInt();
edge = new Vector<Vector<Edge>>();
for (int i = 0; i < V + 1; i++) {
Vector<Edge> e = new Vector<Edge>();
edge.add(e);
}
for (int i = 0; i < E; i++) {
int u = scanner.nextInt();
int v = scanner.nextInt();
int d = scanner.nextInt();
Edge e = new Edge(v, d);
edge.elementAt(u).add(e);
}
Vector<Integer> dist = dijkstra(start);
for (int i = 1; i < dist.size(); i++) {
System.out.println(String.valueOf(dist.elementAt(i)));
}
}
public static Vector<Integer> dijkstra(int cur) {
PriorityQueue<Edge> pq = new PriorityQueue<>();
Vector<Integer> dist = new Vector<Integer>();
for (int i = 0; i < V + 1; i++) { // dist배열 초기화
if (i == cur)
dist.add(0);
else
dist.add(-1);
}
Edge e = new Edge(cur, 0);
pq.add(e); // 맨처음 (1,0) 넣음
while (!pq.isEmpty()) {
Edge here = pq.remove();
for (int i = 0; i < edge.elementAt(here.dst).size(); i++) { // 연결된 정점만큼
Edge a = edge.elementAt(here.dst).elementAt(i); // 연결된 정점 차례대로 넣음
int there = a.dst; // 1로 시작했다면 연결된 2,3,7 들어갈것
int nextdist = dist.elementAt(here.dst) + a.weight; // 현재까지의거리+연결된간선weight (=정점확장시 총weight)
if (dist.elementAt(there) == -1 || dist.elementAt(there) > nextdist) { // 미방문이거나 or nextdist가 기존거리보다 작다면
dist.setElementAt(nextdist, there); // setElementAt(E obj, int index)
Edge ne = new Edge(there, nextdist);
pq.add(ne); // dist 거리정보 배열 업데이트해주고, pq에도 추가
}
} // 처음 1들어갔을때 2,3,7로 for문 3번돌고 다시 while문 돌며 pq.remove()로 pq풀안의 3개중 하나 뽑아내며 다시 반복 ㄱㄱ
}
return dist;
}
}

Floyd-Warshall Algorithm
그래프에서 모든 정점사이의 최단거리를 구하는 알고리즘
(Dijkstra Alg을 모든 정점에서 동작시키면 같은결과를 가져오나, F-W 알고리즘이 더 간결하다)
(또 Dijkstra는 음수weight가 있으면 제대로 동작하지않으나, F-W는 음의사이클만 없다면 음수weight가 있어도 동작한다)
- 모든 정점쌍 (i,j)에 대해, k라는 경유지를 거쳤을때 기존의거리보다 짧아진다면 최단거리를 갱신
- 시간복잡도=O(V3)
|
Input |
Output |
|
첫번째 줄에 그래프의 크기 N이 주어지고, 두번째 줄부터 N + 1 줄 까지 인접행렬이 주어진다. 인접행렬의 값이 0이면 해당 경로가 없음을 의미한다. |
그래프의 모든 쌍의 최단경로를 인접행렬 형태로 출력한다. |
import java.util.*;
public class Test {
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int d[][] = new int[n + 1][n + 1];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
d[i][j] = scanner.nextInt();
if (d[i][j] == 0) d[i][j] = Integer.MAX_VALUE;
}
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if (d[i][k] == Integer.MAX_VALUE || d[k][j] == Integer.MAX_VALUE) continue; // 0만나면 패스
if (d[i][j] > d[i][k] + d[k][j]) // k를 거치는 경로가 더 짧으면 그 값으로 업데이트
d[i][j] = d[i][k] + d[k][j];
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++)
System.out.print(d[i][j] + " ");
System.out.println();
}
}
}
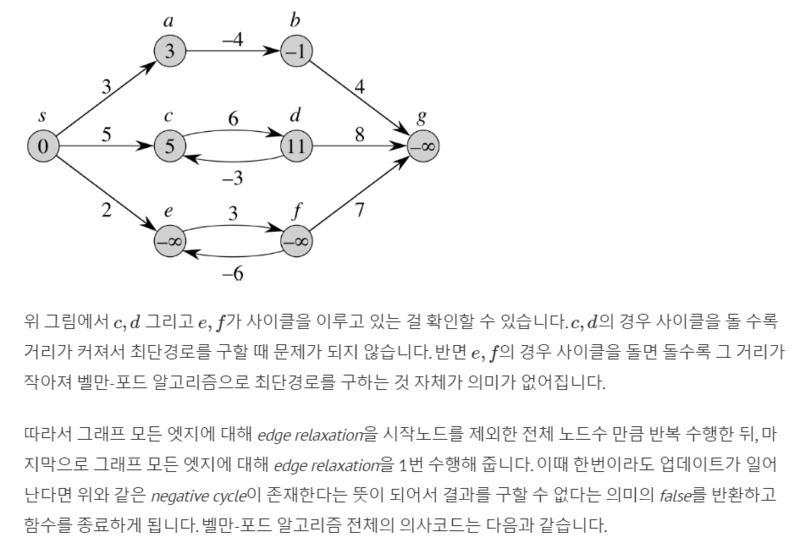
Bellman-Ford Algorithm
Dijkstra와 마찬가지로, 한 정점에서 나머지 정점까지 거리를 구하는 알고리즘
대신 dijkstra와 달리, 음수weight를 갖는 그래프에서도 동작하며, 음수사이클을 찾아내는 기능도 한다.
수행시간은 dijkstra보다 느리다.
기본적인 아이디어는 dijkstra와 비슷하게, distance배열을 만들어서 최단거리에 근접하게 계속 갱신시킨다.
하지만, priority queue로 간선에 연결된 정점의 최단거리를 갱신하는것이 아니라, 모든 정점의 최단거리를 구할때까지 모든 간선들을 여러번 확인하여 최단거리를 구한다.
dijkstra와 비슷한 전처리과정으로 distance배열을 만들고 시작정점의 distance는 0으로 설정한뒤 모든간선을 확인한다. 간선이 u->v라면, distance[v]와 distance[u]+weight[E]를 비교해 갱신한다. 이러한 과정을 V번 반복한다. V번 반복하는 이유는, dijkstra처럼 제한이없을경우 음수사이클때문에 새로운최단거리를 계속찾아 무한히 갱신하게 된다. 따라서 V번의 제한을 두며, 이때 V-1번이 아닌 V번인 이유는 음수사이클이 없는 정상적인 경우라면 V-1번만에 완성되지만, 음수사이클이 있다면 V번째에 갱신이 되기 때문이다. 이를통해 음수사이클을 판별한다.
|
Input |
Output |
|
첫 줄에 정점의 개수 N과 간선의 개수 M, 그리고 시작 정점 S가 주어집니다. 다음 M줄에 간선의 관계 시작정점 u와 도착정점 v 그리고 간선 가중치 w가 주어집니다. |
시작정점에서 각 정점사이의 거리를 모두 출력합니다. 만약 음수 사이클이 발견되면 -1을 출력합니다. |
import java.util.*;
class Edge {
int dst, weight;
Edge(){}
Edge(int dst, int weight) {
this.dst = dst;
this.weight = weight;
}
}
public class Test {
static Vector<Vector<Edge>> edge;
static int V;
static int E;
static int s;
private static int INF = 987654321;
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
V = scanner.nextInt();
E = scanner.nextInt();
s = scanner.nextInt();
edge = new Vector<Vector<Edge>>();
for (int i = 0; i < V + 1; i++) {
Vector<Edge> e = new Vector<Edge>();
edge.add(e);
}
for (int i = 0; i < E; i++) {
int u = scanner.nextInt();
int v = scanner.nextInt();
int d = scanner.nextInt();
Edge e = new Edge(v, d);
edge.elementAt(u).add(e);
}
Vector<Integer> dist = bellmanFord(s);
if (dist == null) {
System.out.println(-1);
}
else {
for (int i = 1; i < dist.size(); i++) {
System.out.println(String.valueOf(dist.elementAt(i)));
}
}
}
public static Vector<Integer> bellmanFord(int cur) {
Vector<Integer> upper = new Vector<Integer>();
for (int i = 0; i <= V; i++) {
if (i == cur) upper.add(0);
else upper.add(INF);
}
boolean updated = false;
for (int iter = 0; iter < V; iter++) {
updated = false; // iter가 V-1번 수행된뒤, 음수사이클이 없다면 V번째에는 업데이트가 일어나지않아야한다. updated=false로 유지됨. for문안에 들어가서 true로 바뀌었다는건 음수사이클이 존재한다는것, 뒤에서 null 반환.
for (int here = 1; here <= V; here++) { // 이전알고리즘들과 비슷한 역할. here과 연결된 것들 차례대로 보며 거리 더 짧으면 갱신.
for (int i = 0; i < edge.elementAt(here).size(); i++) {
Edge a = edge.elementAt(here).elementAt(i);
int there = a.dst;
int nextdist = upper.elementAt(here) + a.weight;
if (upper.elementAt(there) > nextdist) {
upper.setElementAt(nextdist, there);
updated = true;
}
}
}
if (!updated) break; // 물론 다돌기전에 갱신이 끝나면 for문 나가서 그대로 작업을 완료하고 결과물 리턴.
}
if (updated) return null;
return upper;
}
}

'Algorithm' 카테고리의 다른 글
| 알고리즘) DP (Dynamic Programming, 동적계획법), ex: Coin Change Problem (0) | 2019.09.13 |
|---|---|
| 알고리즘) Disjoint-set Algorithm (서로소 집합 알고리즘) (0) | 2019.09.13 |
| 알고리즘) Graph - MST (Minimum_Cost Spanning Tree) using Prim/Kruskal's Algorithm (0) | 2019.09.13 |
| 알고리즘) Graph - DFS, BFS (깊이우선탐색, 너비우선탐색) (0) | 2019.09.12 |
| 알고리즘) Two Pointer, Sliding Window (0) | 2019.09.12 |
- Total
- Today
- Yesterday
- FRAGMENT
- 우아한 테크코스
- Algorithm
- graph
- 프로그래머스
- socket
- C
- reversing
- javascript
- brute-force
- Stack
- dfs
- bfs
- Android
- mysql
- sort
- 해외여행
- OneToMany
- webhacking.kr
- 개발자
- 웹해킹
- Vo
- git
- Data Structure
- 회고
- queue
- Android Studio
- 리버싱
- Java
- JPA
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
