티스토리 뷰
Dynamic Programming (동적계획법)
복잡한 문제를 여러개의 작은부분문제(sub-problem)으로 나누어 해결하는 기법.
이미 계산된 부분 문제가 다시 발생하면, 새롭게 계산하지않고 이전의 계산값을 참조해 이용할 수 있다.
DP를 통해 부분문제를 다시 해결하는 시간을 절약할 수 있지만, 이전 계산값을 저장할 공간이 필요하므로 Time - Space간의 trade off라고 할 수 있다.
ex. 피보나치
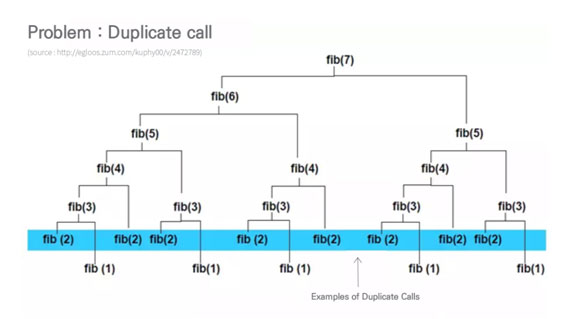
단순탐색으로 구현시, 위와 같이 여러번 계산된다.
=> Memorization : 한번 계산된 값을 기록해두고 이후 중복호출 되었을때 새롭게 계산하는게 아닌 저장해둔값을 가져와 사용한다.

fibonacci_topdown
Top-Down / Bottom-Up
Top-down 방식은 큰 문제에서 작은 부분문제를 재귀적으로 호출하여 리턴되는 값을 이용해 큰 문제를 해결한다.
위의 피보나치 그림이 이에 해당한다.
Bottom-up 방식은 작은 부분문제들을 미리 계산해두고, 이 부분문제들을 모아 큰 문제를 해결한다.
일반적으로 배열에 값을 채워나가며, 이 방식으로 피보나치를 구현하면 아래와 같다.

fibonacci_bottomup
두 방법은 장단점이 존재한다.
Top-down방식은 재귀함수로 구현되므로 함수호출에 대한 오버헤드가 발생한다.
반면 Bottom-up방식은 반복문으로 구현되므로 비교적 시간 및 메모리의 최적화가 쉽다.
하지만, Bottom-up방식은 (큰 문제를 해결하기까지 어떤 sub-problem이 요구되는지 알수없으므로) 모든 부분문제를 계산해야한다. 반면 Top-down방식은 큰 문제를 해결하는데 필요한 sub-problem만을 호출해 계산하므로, 상황에 따라 Bottom-up방식보다 빠를 수 있다.
Example : Coin Change Problem (동전 교환 문제)
동전의 종류와 금액이 주어졌을때, 특정 금액을 만들기위한 동전의 최소 개수를 구하는 문제
1, 5, 12원짜리 동전이 있고 15원을 만드는 경우라면, 먼저 가장 큰 동전부터 사용하는 Greedy한 방법이 있다. 이 경우 12+1+1+1로 4개를 사용한다. 하지만 최적값은 5+5+5의 3개이다. Greedy한 방법은 결국 최적값이라는 확신을 얻기위해 모든 경우를 계산하게 된다.
따라서 이때 DP를 사용한다. K원을 만들기 위해, 'K-동전1개'원을 만드는 방법수에 1(뺀 동전1개)을 더하는 방법을 사용한다. 이전계산값을 활용한 bottom-up방식 DP이다. 피보나치 그림을 보며 잘 이해해보자.
Input | Output |
첫 줄에 동전의 개수 N과 만들어야 하는 금액 K가 주어집니다. (1 ≤ N ≤ 100, 1 ≤ K ≤ 10,000) 둘째 줄에 N개의 동전의 금액이 주어집니다. 모든 동전의 금액은 10,000보다 작거나 같은 양의 정수입니다. | K원을 만들기 위해 필요한 동전의 최소개수를 출력합니다. 만약 K원을 만드는게 불가능하다면 -1을 출력합니다. |
import java.util.*;
public class Test {
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
int Coin[] = new int[n];
for (int d = 0; d < n; d++) {
Coin[d] = scanner.nextInt();
}
int D[] = new int[k + 1];
for (int d = 1; d <= k; d++) { // D[]의 인덱스 d
D[d] = -1; // 일단 -1로 초기화
for (int c = 0; c < n; c++) { // Coin[]의 인덱스 c
if (Coin[c] <= d) { // 일단 궁금한 d원이 갖고있는 동전 Coin[c]들보다 커야함. 갖고있는 동전보다 작은 값은 당연히 못만들어냄. -1 그대로 리턴
if (D[d - Coin[c]] < 0) continue; // D배열은 어짜피 최소개수라 양의값을 가지므로 0보다 작다는건 -1이라는것이다. 따라서 d-Coin[c]원을 만드는 방법이 없다면 => 패스 // 반대로 보면, d-Coin[c]원을 만드는 방법이 없는데 여기에 어떤 Coin[c] 코인1개를 더해본들 여전히 못만든다.
if (D[d] < 0) D[d] = D[d - Coin[c]] + 1; // 위의 두 if문을 통과해 이제 만들수있는 상태다. D[d]가 -1이라면, 즉 구하려는 d원을 처음만났다면 일단 'd-Coin[c]원의 방법에 Coin[c]코인 1개를 더하는 방법'으로 값을 할당한다. 예를들어 15원을 만들려면 15원-1원=14원 의'방법수'에 1원을 하나 더해서 만들자는 것.
else if (D[d - Coin[c]] + 1 < D[d]) D[d] = D[d - Coin[c]] + 1; // 바로위에서 Coin[0]을 이용해 값을 할당하고 for문으로 다시 왔다고 생각해보자. Coin[1]을 이용한 방법이 더 효율적일수있다. 이런 경우를 위해 새롭게 구한값인 D[d-Coin[c]]+1이 기존의 D[d]보다 작다면, 이 값을 D[d]에 넣어준다.
}
}
}
System.out.println(D[k]);
}
}
'Algorithm' 카테고리의 다른 글
| 알고리즘) Permutation, Combination (순열, 조합) (0) | 2019.09.13 |
|---|---|
| 알고리즘) 5 DP Examples - Knapsack, LCS, LIS, Edit Distance, Matrix Chain Multiplication (0) | 2019.09.13 |
| 알고리즘) Disjoint-set Algorithm (서로소 집합 알고리즘) (0) | 2019.09.13 |
| 알고리즘) Graph - Dijkstra/Floyd-Warshall/Bellman-Ford 's Alg (distance) (0) | 2019.09.13 |
| 알고리즘) Graph - MST (Minimum_Cost Spanning Tree) using Prim/Kruskal's Algorithm (0) | 2019.09.13 |
- Total
- Today
- Yesterday
- OneToMany
- 회고
- reversing
- Stack
- 개발자
- javascript
- Android Studio
- Vo
- 우아한 테크코스
- Algorithm
- queue
- Data Structure
- dfs
- JPA
- 프로그래머스
- Java
- 웹해킹
- C
- Android
- brute-force
- FRAGMENT
- socket
- sort
- graph
- mysql
- git
- 리버싱
- 해외여행
- bfs
- webhacking.kr
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
