티스토리 뷰
Disjoint-set Algorithm (서로소 집합 알고리즘)
집합, 그룹을 관리하는 알고리즘
각 그룹을 트리구조로 관리
크게 2가지의 연산으로 구성된다.
find(x) : x번 노드의 root를 찾는 함수
link(x, y) : x 노드가 속한 그룹과 y 노드가 속한 그룹을 합치는(연결하는) 함수
또한 위 연산을 위해, parent[i] : i번 노드의 부모로 정의되는 배열이 사용된다.
아래의 내용은 codeground 사이트에서 가져온 내용
Disjoint-Set
서로소 집합(Disjoint-Set)은 집합, 혹은 그룹을 관리하는 효율적인 알고리즘입니다.
각각의 그룹을 트리 구조로 관리하는 이 알고리즘은 크게 두 가지의 연산을 가집니다.
find(x): x번 노드의 최고 조상(루트)을 찾는 함수
link(x, y): x노드가 속한 그룹과 y노드가 속한 그룹을 합치는(잇는) 함수
또한 위 연산들을 구현하기 위해 par[i]: i번 노드의 부모로 정의되는 배열을 가집니다.
예를 들어 1~5번의 번호를 가진 사람이 있다고 합시다.
처음에 5명의 사람들은 모두 각자 독립적인 1인 그룹이 됩니다.
각 그룹을 정점으로 표현하면 아래와 같습니다.

또한 초기 par배열은 다음과 같습니다.

이 상태에서 1번이 속한 그룹과 2번이 속한 그룹을 합치는 link(1, 2) 연산을 수행해봅시다.
두 정점이 같은 집합임을 나타내기 위해 간선으로 이어준 뒤, par[2]의 값을 1로 바꿔줍니다.


link(1, 2)
이후 link(3, 4), link(4, 5) 연산을 수행해봅시다.
마찬가지로 3번과 4번, 4번과 5번 정점이 이어지고, par[4]의 값을 3으로, par[5]의 값을 4로 바꿔줍니다.

link(3, 4), link(4, 5)
이처럼 link(x, y) 연산은 y의 부모를 x로 바꿔줌으로서 구현할 수 있습니다.
이를 코드로 구현하면 아래와 같은 함수가 될 것입니다.
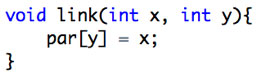
이제 find 연산에 대해서 알아봅시다.
위 상태에서 5번의 최고 조상인 3을 찾기 위한 연산 find(5)는 다음과 같은 과정을 거칩니다.
find(5) => find(par[5]) = find(4) => find(par[4]) = find(3) => 3
위와 같이 find연산은 x의 부모를 찾고, x의 부모의 부모를 찾고, 그 부모를 찾아 최상위 노드(루트)까지 도달할 수 있습니다.
이때 루트 노드랑 par[i]의 값이 i와 같은 노드를 의미합니다.
이를 코드로 구현하면 아래와 같은 함수가 될 것입니다.

이제는 크기가 2이상인 그룹 간의 연결에 대해 알아봅시다.
위 상태에서 link(2, 4)의 연산은 어떻게 동작해야 할까요?
위에서 소개한 link(x, y)함수로는 par[4]를 2로 바꾸기 때문에 기존에 par[4]: 3이라는 정보로 연결되어 있던 간선이 사라지고, 아래와 같이 변화합니다.
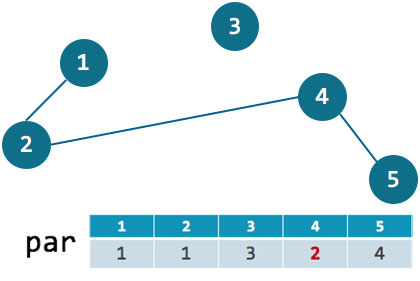
link(2, 4) …?
기존에 3번과 4번은 같은 그룹에 있었습니다.
같은 그룹이라는 것은 서로 같은 트리에 속한다는 의미이며, 같은 트리에 속하는 두 정점은 find연산의 결과값인 정점이 속한 트리의 루트가 같습니다.
하지만 위와 같은 상황에서 find(3): 3과 find(4): 1는 서로 다른 값을 가지게 됩니다.
이는 기존에 y가 속한 그룹 Y의 일부만 x의 서브트리로 연결되기 때문입니다.
이런 현상을 해결하기 위해서는 어떻게 하면 될까요? 간단합니다.
그룹 Y의 일부가 아닌 그룹 Y의 전체, 즉 그룹 Y의 루트를 x의 서브트리로 연결합니다.
즉 link(2, 4)는 link(2, find(4))가 되며 이는 link(2, 3)으로 의미에 맞게 짠 link함수라면 위의 모양이 아닌 아래와 같은 모양이 되어야 할 것입니다.

link(2, 4)
따라서 link(x, y)연산은 다음과 같이 바뀌어야 합니다.

위와 같은 상황에서 다시 한 번 find 연산에 대해 생각해봅시다.
find(5)의 동작은 다음과 같은 과정을 거치게 됩니다.
find(5) => find(par[5]) = find(4) => find(par[4]) = find(3)
=> find(par[3]) = find(2) => find(par[2]) = find(1) => 1
위 과정을 통해 알 수 있듯이 트리의 높이가 커질수록 find연산의 복잡도는 증가하게 됩니다.
만약 위의 예제처럼 트리가 편향적으로 만들어진다면 find연산의 시간 복잡도는 매번 O(N)이 될 것입니다.
이러한 시간 복잡도를 완화하기 위해 우리는 트리의 높이를 최대한 낮게 관리하는 것이 좋습니다.
예를 들어, link(2, 4)의 연산을 다시 살펴봅시다.
우리는 Y그룹을 x의 서브트리로 연결하였습니다.
하지만 이보다는 Y그룹을 x의 루트의 서브트리로 연결하는 편이 트리의 높이를 더 낮출 수 있는 방법이 될 것입니다.
즉, link(2, 4)는 link(2, find(4))보다 link(find(2), find(4)) = link(1, 3)가 되었을 때가 더 유리합니다.

link(2, 4)
link함수 역시 다음과 같이 바뀔 수 있습니다.

또한 우리는 find(5) 연산이 재귀호출됨에 따라 find(5) = find(4) = find(3) = find(2) = find(1) = 1이라는 루트 값을 매번 재귀 호출의 반환값에서 알 수 있습니다.
우리가 지금 하려는 것은 집합에 관한 연산입니다.
즉 par배열은 루트를 찾기 위한 용도로 사용될 뿐, 직계 부모-자식 관계는 의미가 없습니다.
따라서 각 재귀호출에서 반환된 루트값을 par[x]에 바로 연결함으로써 트리를 다음과 같이 변화시킬 수 있습니다.

이러한 작업을 find 함수 안에 구현하면 다음과 같습니다.

위 코드를 이용하면 아무리 편향된 트리라도 find연산은 한 번 호출 된 이후 그 복잡도가 대폭 줄어들게 됩니다.
아래는 서로소 집합을 구현한 코드입니다.
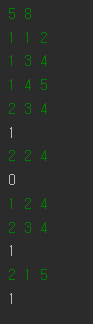
Input | Output |
첫 줄에 정점의 개수 N과 명령어의 수 Q가 주어집니다. (1 ≤ V ≤ 100,000, 1 ≤ Q ≤ 100,000) 둘째 줄에 Q개의 줄에 걸쳐 다음과 같은 명령어가 들어옵니다. 1 x y: x가 속한 그룹과 y가 속한 그룹을 합칩니다. 2 x y: x와 y가 같은 그룹에 속해있다면 1, 아니라면 0을 출력합니다. | 명령어의 결과를 출력합니다. |
import java.util.*;
public class Test {
static int par[] = new int[100001];
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int q = sc.nextInt();
for (int i = 1; i <= n; i++) {
par[i] = i;
}
while (q-- > 0) {
int cmd = sc.nextInt();
int x = sc.nextInt();
int y = sc.nextInt();
if (cmd == 1) {
link(x, y);
} else {
if (find(x) == find(y)) {
System.out.println(1);
} else {
System.out.println(0);
}
}
}
}
public static int find(int x) {
if (par[x] == x) return x;
else return par[x] = find(par[x]);
}
public static void link(int x, int y) {
par[find(y)] = find(x);
}
}
'Algorithm' 카테고리의 다른 글
- Total
- Today
- Yesterday
- bfs
- javascript
- socket
- brute-force
- sort
- queue
- reversing
- Data Structure
- Algorithm
- graph
- 리버싱
- 프로그래머스
- dfs
- Vo
- 회고
- 해외여행
- OneToMany
- FRAGMENT
- C
- JPA
- git
- Java
- 개발자
- Stack
- 웹해킹
- Android
- Android Studio
- mysql
- 우아한 테크코스
- webhacking.kr
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
