티스토리 뷰
Data Structure
자료구조) Tree - Binary Search Tree, Segment Tree, Binary Indexed Tree
os94 2019. 9. 12. 19:20Binary Search Tree (이진 탐색 트리)
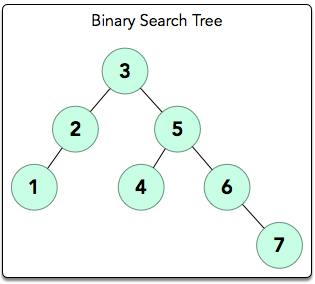
def
모든 원소는 서로다른 유일한 값.
왼쪽 subtree의 값은 그 root보다 작다.
오른쪽 subtree의 값은 그 root보다 크다.
왼/오른쪽 subtree도 Binary Search Tree이다.
탐색/삽입/삭제 중 삭제연산이 번거롭다. 노드를 삭제한 후에도 BST를 유지해야하므로 후속조치가 필요하다.
삭제할 노드가 1. degree=0(leaf node)인지 2. degree=1인지 3. degree=2인지에 따라 달라짐.
Segment Tree
구간의 정보를 빠르게 구할수있는, Complete Binary Tree 형태의 자료구조
Example) 구간 최소값을 구하는 Segment Tree
구하려는 데이터 배열을 완전이진트리의 최하단에 배치하고, 부모노드는 자식노드들중 가장 작은값을 갖게 구성하여 트리를 완성시킨다.

구간 최소값을 구하는 Segment Tree
Binary Indexed Tree = fenwick Tree
Segment Tree와 비슷하게 구간의 정보를 저장할수있는 자료구조
구간 합 등을 알아내는데 이용된다.
Segment Tree보다 간단하지만, ST가 BIT보다 좀더 다양한 목적으로 사용가능하다.



- 8번지의 검정박스는, 8번지의 데이터가 1~8까지의 합을 축적하고있음을 의미
- 파란박스를 보면, 1은 1,2,4,8,16번지에 더해졌음을 의미
- 청록박스를 보면, 1~11번지까지의 합은 8,10,11번지의 합을 구하면 된다
'Data Structure' 카테고리의 다른 글
| 자료구조) Graph (그래프) (0) | 2019.09.12 |
|---|---|
| 자료구조) Tree - Heap, Priority Queue (힙, 우선순위 큐) (0) | 2019.09.12 |
| 자료구조) Tree, Binary Tree (트리, 이진트리) (0) | 2019.09.12 |
| 자료구조) Hash (해시) (0) | 2019.09.12 |
| 자료구조) Stack, Queue (스택, 큐) (0) | 2019.09.12 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- dfs
- OneToMany
- Android
- Android Studio
- 리버싱
- reversing
- Java
- Vo
- queue
- mysql
- graph
- 프로그래머스
- 회고
- 개발자
- Stack
- Data Structure
- 웹해킹
- brute-force
- C
- sort
- 우아한 테크코스
- JPA
- socket
- git
- 해외여행
- bfs
- FRAGMENT
- javascript
- Algorithm
- webhacking.kr
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
