티스토리 뷰
Tree
용어 : Root, Child, Parent, Siblings, Leaf=Terminal, Branch=Internal, Degree, Height, Level
=> 모든 노드의 Degree(차수)가 2이하
Binary Tree
구현
- 순차 자료구조 (ex. 배열)
Node (of Node i) | Index | Condition |
Parent | floor( i/2 ) | i > 1 |
Left Child | 2i | 2i ≤ n |
Right Child | 2i+1 | (2i+1) ≤ n |
Root | 1 | 0 < n |
- 연결 자료구조 (ex. 하단 코드)
class TreeNode {
Object data;
TreeNode left;
TreeNode right;
}Traversal (순회)
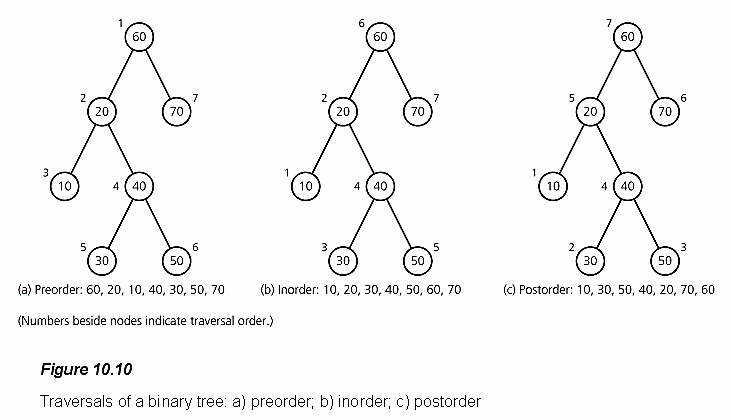
: Pre-order, In-order, Post-order
D
L R
(D : 현재노드, L : 왼쪽 서브트리, R : 오른쪽 서브트리)
Pre-order Traversal (전위 순회) : DLR 순서
PreOrder(현재 트리 노드의 위치 cur){ Print(cur’s value) If(cur’s left exist){ Pre-Order(cur->left) } If(cur’s right exist){ Pre-Order(cur->right) } }In-order Traversal (중위 순회) : LDR 순서
InOrder(현재 트리 노드의 위치 cur){ If(cur’s left exist){ In-Order(cur->left) } Print(cur’s value) If(cur’s right exist){ In-Order(cur->right) } }Post-order Traversal (후위 순회) : LRD 순서
PostOrder(현재 트리 노드의 위치 cur){ If(cur’s left exist){ Post-Order(cur->left) } If(cur’s right exist){ Post-Order(cur->right) } Print(cur’s value) }
실습

Input | Output |
첫 줄에 트리 노드의 개수 N이 주어집니다. (1 ≤ N ≤ 1,000) 두번째 줄부터 N개의 줄에 0번째 노드부터 N-1번째 노드의 부모 노드가 주어집니다. (-1일 경우 해당 노드가 루트 노드임을 의미합니다.) | 각 해당 트리 구조의 Pre-Order, In-Order, Post-Order Traversal 결과를 출력합니다. |
import java.util.*;
public class Test {
static final int EMPTY = -1;
static final int TREE_MAX_SIZE = 10000;
static int child[][];
static int root = 0, N, P;
static void insert(int parent_idx, int child_idx) {
if (parent_idx == -1) root = child_idx;
else if (child[parent_idx][0] == EMPTY) {
child[parent_idx][0] = child_idx;
}
else if (child[parent_idx][1] == EMPTY) {
child[parent_idx][1] = child_idx;
}
else {
// tree_node has left, right
}
}
static void pre_order(int cur) {
int left = child[cur][0];
int right = child[cur][1];
System.out.print(String.valueOf(cur) + ' ');
if (left != EMPTY) {
pre_order(left);
}
if (right != EMPTY) {
pre_order(right);
}
}
static void in_order(int cur) {
int left = child[cur][0];
int right = child[cur][1];
if (left != EMPTY) {
pre_order(left);
}
System.out.print(String.valueOf(cur) + ' ');
if (right != EMPTY) {
pre_order(right);
}
}
static void post_order(int cur) {
int left = child[cur][0];
int right = child[cur][1];
if (left != EMPTY) {
post_order(left);
}
if (right != EMPTY) {
post_order(right);
}
System.out.print(String.valueOf(cur) + ' ');
}
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
child = new int[TREE_MAX_SIZE][2];
for (int i = 0; i < TREE_MAX_SIZE; i++)
for (int j = 0; j < 2; j++)
child[i][j] = EMPTY;
N = scanner.nextInt();
for (int i = 0; i < N; i++) {
P = scanner.nextInt();
if (P == -1) {
root = i;
}
else {
insert(P, i);
}
}
pre_order(root);
System.out.println("");
in_order(root);
System.out.println("");
post_order(root);
System.out.println("");
}
}

Special case
- Full Binary Tree
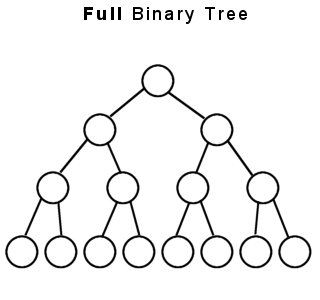
모든 노드가 포화.
최대 노드 수 : 2^(h+1)-1
- Complete Binary Tree

Full BT에서 뒤에서부터 몇개 빠진 형태
노드 수가 n개일때,
Full BT에서 1번 - n번 노드는 위치가 일치하고
n+1번 - 2^(h+1)-1번 노드는 공백
- Skewed Binary Tree
- Heap
- Binary Search Tree
- Segment Tree
- Binary Indexed Tree
'Data Structure' 카테고리의 다른 글
| 자료구조) Tree - Binary Search Tree, Segment Tree, Binary Indexed Tree (0) | 2019.09.12 |
|---|---|
| 자료구조) Tree - Heap, Priority Queue (힙, 우선순위 큐) (0) | 2019.09.12 |
| 자료구조) Hash (해시) (0) | 2019.09.12 |
| 자료구조) Stack, Queue (스택, 큐) (0) | 2019.09.12 |
| 자료구조) List (리스트) (0) | 2019.09.12 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- Android Studio
- Vo
- 프로그래머스
- 리버싱
- Stack
- 우아한 테크코스
- queue
- 해외여행
- 웹해킹
- OneToMany
- brute-force
- Data Structure
- webhacking.kr
- graph
- C
- Java
- git
- sort
- socket
- reversing
- bfs
- mysql
- 회고
- JPA
- FRAGMENT
- javascript
- dfs
- Algorithm
- Android
- 개발자
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
