티스토리 뷰
Network/Maximum Flow
유량그래프 : 간선의 weight가 정점에서 정점으로 보낼수있는 최대유량을 의미하는 그래프
최대유량 : 해당 간선을 통해 동시에 흘려보낼수있는 물의 최대치
이러한 유량그래프에서, Source정점에서 Sink정점까지 최대 얼마만큼의 유량이 지나갈수있는지에 관한 문제를 Network/Maximum Flow라고 한다.
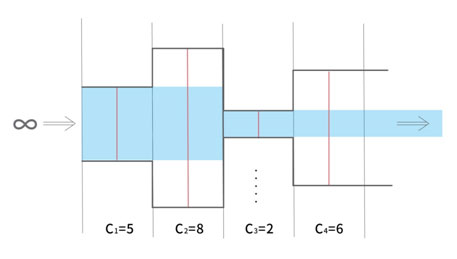
아래와 같이, 수로(간선)에 1초마다 지날수있는 물의 최대치가 정의되어있다면, 수로는 자신의 용량이상의 물은 통과 시킬수없다. 따라서 결과적으로 통과할수있는 물의 최대량은 왼쪽은 2, 오른쪽은 4이다.

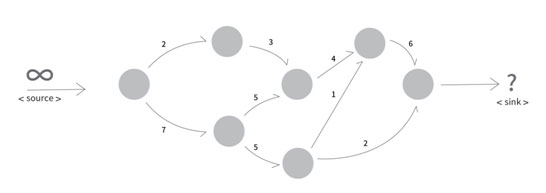
따라서 위의 그래프를 Maximum Flow(최대유량)으로 보내면 그 값은 7이다.
좌측값은 실제로 해당 간선에 흐른 유량(flow), 우측값은 해당 간선의 최대유량(capacity)이다.
(source에서 위로2만큼&아래로5만큼 보내서 총7만큼 sink로 보내는것이, 물을 넘쳐서 버리거나 부족해서 빈공간이 없는 최적의 효율적인 양인것)

1. Ford-Fulkerson Algorithm (using DFS)
먼저 잔여간선에 대해 알아보자.
잔여간선(Residual Edge) : flow의 반대방향으로 존재하는 간선으로, 그 weight는 흐르는 flow의 양과 같다.

같은 유량그래프라도 아래의 A, B와 같이 다양한 경우가 있다.
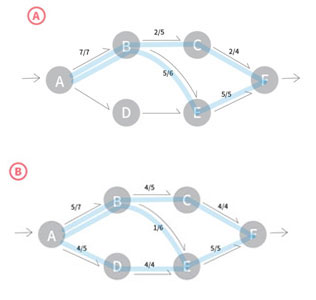
A의 상태에서 DFS방법을 사용해 점차적으로 최적의 경우인 B로 개선하는것이 Ford-Fulkerson Algorithm이다.
A같은 경우가 발생하는것은 물이 단방향으로 흘러 한번 흐른 유량의 방향을 바꿀수없기 때문이다. 따라서 잔여간선을 이용해, 한번 흐른 물을 다시 되돌려보내 다른 방향으로 보낼수있도록 한다. 이렇게 우회경로를 찾는다.
(즉, 잔여간선은 "현재 A->B로 5의 유량이 흐른다면, 경우에 따라 B로 들어오는 유량을 최대 5까지 줄여 A에서 다른정점으로 흘려보낼수있다"라는 의미를 갖게한다.)

기존 그래프에서 잔여간선을 추가해, 새로운 A-D-E-B-C-F의 경로가 생기게 된다.
이 경로에 대해 2만큼의 유량을 보내, 위에서 9라는 최적의 경우를 만들어낼수있다.
DFS 방법으로,
source에서 시작해 sink를 만날때까지 flow를 추가로 흘릴수있는 간선들을 이용해 (cycle 없도록) 탐색한다.
sink에 도달했을때, 이제까지 거쳐온 간선들에 흘릴수있는 [최대 유량] [1](기존상태에서 추가로 더 흘릴수있는)만큼을, 해당 경로로 흘린다. 이때 당연히 잔여간선도 갱신한다.
이러한 탐색과정을 반복하다가, 더이상 갱신가능한 경로가(source-sink로 새로운 경로가) 발견되지않으면 알고리즘을 종료한다.
[1]: 새로 발견한 경로를 이용할것이므로, 가능한 한도내의 최대 유량을 보낸다. 이때 수치상으론 거쳐온 간선들의 가능한 유량값들중 최소값이 이에 해당
문제점
O(F*E)의 시간복잡도를 갖는다. (F : 그래프에 흐를수있는 최대 용량)
아래와 같은 최악의 경우가 발생할수있기 때문.

경로 ABD와 ACD만 찾으면, 1000+1000=2000의 최적값을 바로 찾을수있는데,
AB사이를 이용하면, SABT와 SBAT로 1씩 보내는 과정을 1000번씩 반복해 총 2000번 loop을 돌수도있다,,,
따라서 다음과 같이 BFS를 이용한 방법이 등장.
2. Edmond-Karp Algorithm (using BFS)
BFS의 특성상, 간선의 수가 적은 경로를 우선적으로 발견하여 앞의 최악의 경우가 발생하지 않는다.
이 경우, 최악의 상황에서도 O(V*E2)로 동작
=> 유량이 매우 작은 간선으로만 이뤄진 그래프에선 DFS로, 반대로 유량이 큰 그래프에선 BFS로 구현하는것이 유리하다
탐색과정은 전과 비슷하며, 다만 BFS이므로 탐색이 완료되었을때 목적지~출발점까지의 사용한 간선들을 역추적할수있도록 이전노드에 대한 정보를 함께 기록한다.
Input | Output |
첫 줄에 정점의 개수 V와 간선의 개수 E가 주어집니다. (1 ≤ V ≤ 100, 1 ≤ E ≤ 1,000) 두번째 줄에는 Source 정점의 번호 S1과 Sink정점의 번호 S2가 주어집니다. (1 ≤ S1, S2 ≤ V) 세번째 줄부터 E개의 줄에 걸쳐 간선의 정보가 F, T, C가 들어옵니다. 이는 F정점으로부터 T정점으로 가는 용량이 C인 간선이 존재한다는 의미입니다. (1 ≤ F, T ≤ V, 1 ≤ C ≤ 100) | 주어진 유량그래프의 최대유량을 출력합니다. |


import java.util.*;
import java.lang.*;
public class Test {
static List<NetworkEdge>[] adj = new ArrayList[101];
static boolean chk[] = new boolean[101];
static int src, sink;
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int v = sc.nextInt();
int e = sc.nextInt();
for (int i = 1; i <= v; i++) {
adj[i] = new ArrayList<NetworkEdge>();
}
src = sc.nextInt();
sink = sc.nextInt();
for (int i = 0; i < e; i++) {
int from = sc.nextInt();
int to = sc.nextInt();
int capacity = sc.nextInt();
adj[from].add(new NetworkEdge(to, capacity, 0, adj[to].size()));
adj[to].add(new NetworkEdge(from, 0, 0, adj[from].size() - 1));
}
int ans = 0, added_flow;
while (0 < (added_flow = find_path(src, 101))) { //한번돌릴때마다 flow가 갱신되며 상태가 달라지므로 find_path가 0 나올때까지 계속 돌리며 찾음
ans += added_flow;
for (int i = 1; i <= v; i++) { //다시 돌리기위한 노드방문여부 초기화
chk[i] = false;
}
}
System.out.println(ans);
}
public static int find_path(int cur, int addible_flow) {
if (cur == sink) return addible_flow; //목적지 도착하면 추가로흘릴수있는flow 리턴
chk[cur] = true; //현재노드 방문했음을 check
for (int i = 0; i < adj[cur].size(); i++) { //adj[cur].size()만큼 loop
NetworkEdge edge = adj[cur].get(i); //edge에 차례대로 가져오며
if (chk[edge.to] || edge.capacity - edge.flow == 0) continue; //연결된 노드가 이미 방문했거나 or flow/capacity가 꽉차있으면 못가므로 pass
int added = find_path(edge.to, Math.min(addible_flow, edge.capacity - edge.flow)); //갈수있으므로, 연결된 노드를 방문하자
if (added > 0) { //방문했으면 갱신해야지
edge.flow += added;
adj[edge.to].get(edge.residual_idx).flow -= added;
return added;
}
}
return 0; //find_path 실패하면 경로가 더이상 존재하지않으므로 0 리턴해 알고리즘 종료
}
static class NetworkEdge {
int to, capacity, flow, residual_idx;
NetworkEdge(){}
NetworkEdge(int t, int c, int f, int ridx) {
to = t;
capacity = c;
flow = f;
residual_idx = ridx;
}
}
}ㄴ Ford-Fulkerson Alg.

네트워크 플로우(Network Flow) 알고리즘,_에드몬드 카프 알고리즘(Edmonds-Karp algorithm)
Bipartite Matching 이분 그래프
이분 그래프 : 두 그룹으로 이뤄진 정점들과, 이 두 그룹을 연결하는 간선들로 이뤄진 그래프
매칭 : A그룹의 정점과 B그룹의 정점을 연결하는것

이때, 모든 정점은 단 하나의 매칭에 속해야 한다. 정점이 중복되어선 안된다.
최대 매칭이란 이분그래프에서 선택할수있는 매칭의 최대갯수를 말하며
, 이러한 문제를 (Maximum) Bipartite Matching이라 한다.
매칭의 최대 개수를 앞에서 다룬 최대 유량 문제를 변형해 접근하자.

source와 sink를 만들어 연결시키고, 모든 capacity를 1로 주면
최대유량문제로 해결할수있다.
Input | Output |
첫 줄에 정점의 개수 V와 간선의 개수 E가 주어집니다. (1 ≤ V ≤ 1,000, 1 ≤ E ≤ 10,000) 두 번째 줄부터 E개의 줄에 걸쳐 V1, V2가 주어집니다. 이는 V1과 V2를 연결하는 간선이 존재한다는 의미입니다. (1 ≤ V1, V2 ≤ V) 입력되는 그래프는 V1집합과 V2집합으로 구분되는 이분 그래프임이 보장됩니다. | 주어진 이분그래프의 최대매칭을 출력합니다. |
import java.util.*;
import java.lang.*;
public class Test {
static List<NetworkEdge>[] adj = new ArrayList[1002];
static boolean chk[] = new boolean[1002];
static int group[] = new int[1002];
static int src, sink;
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int v = sc.nextInt();
int e = sc.nextInt();
for (int i = 0; i <= v + 1; i++) {
adj[i] = new ArrayList<NetworkEdge>();
}
src = 0;
sink = v + 1;
for (int i = 0; i < e; i++) {
int v1 = sc.nextInt();
int v2 = sc.nextInt();
add_edge(v1, v2, 1);
group[v1] = 1;
group[v2] = 2;
}
for (int i = 1; i <= v; i++) {
if (group[i] == 1) {
add_edge(src, i, 1);
}
else if (group[i] == 2) {
add_edge(i, sink, 1);
}
}
int ans = 0, added_flow;
while (0 < (added_flow = find_path(src, 101))) {
ans += added_flow;
for (int i = 0; i <= v + 1; i++) {
chk[i] = false;
}
}
System.out.println(ans);
}
public static void add_edge(int from, int to, int capacity) {
adj[from].add(new NetworkEdge(to, capacity, 0, adj[to].size()));
adj[to].add(new NetworkEdge(from, 0, 0, adj[from].size() - 1));
}
public static int find_path(int cur, int addible_flow) {
if (cur == sink) return addible_flow;
chk[cur] = true;
for (int i = 0; i < adj[cur].size(); i++) {
NetworkEdge edge = adj[cur].get(i);
if (chk[edge.to] || edge.capacity - edge.flow == 0) continue;
int added = find_path(edge.to, Math.min(addible_flow, edge.capacity - edge.flow));
if (0 < added) {
edge.flow += added;
adj[edge.to].get(edge.residual_idx).flow -= added;
return added;
}
}
return 0;
}
static class NetworkEdge {
int to, capacity, flow, residual_idx;
NetworkEdge(){}
NetworkEdge(int t, int c, int f, int ridx) {
to = t;
capacity = c;
flow = f;
residual_idx = ridx;
}
}
}ㄴ 이전과 코드 거의 비슷함

'Algorithm' 카테고리의 다른 글
| 알고리즘) 기하 - Plane Sweeping, CCW, Convex Hull (0) | 2019.09.13 |
|---|---|
| 알고리즘) KMP (Knuth–Morris–Pratt, 문자열 탐색 알고리즘) (0) | 2019.09.13 |
| 알고리즘) Permutation, Combination (순열, 조합) (0) | 2019.09.13 |
| 알고리즘) 5 DP Examples - Knapsack, LCS, LIS, Edit Distance, Matrix Chain Multiplication (0) | 2019.09.13 |
| 알고리즘) DP (Dynamic Programming, 동적계획법), ex: Coin Change Problem (0) | 2019.09.13 |
- Total
- Today
- Yesterday
- 웹해킹
- sort
- queue
- brute-force
- FRAGMENT
- socket
- webhacking.kr
- 회고
- dfs
- 해외여행
- mysql
- git
- C
- Android
- OneToMany
- javascript
- Java
- 개발자
- Vo
- reversing
- 프로그래머스
- Data Structure
- JPA
- Stack
- Algorithm
- graph
- Android Studio
- bfs
- 리버싱
- 우아한 테크코스
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
