티스토리 뷰
Plane Sweeping
직각도형의 넓이를 구할때 쓰이는 알고리즘

곂친 부분이 있기때문에 단순한 공식을 넓이를 구하기 쉽지 않다.
각 직사각형은 4개의 꼭짓점을 가진다. 따라서 n개의 직사각형이라면, 최대 2n개의 x좌표와 2n개의 y좌표가 사용된다.
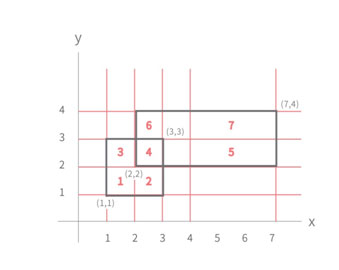
이렇게 각 꼭짓점으로 나누면, 각 영역의 넓이를 구한뒤 그 합으로 정답을 구할수있다.
- 먼저 사용되는 x,y좌표를 모두 구한뒤 정렬시킨다. (원소들이 꼭 유일할 필요는 없다)
- 이후 x,y좌표로 잘려진 영역들을 순회하며, 사각형이 포함되었으면 넓이를 더해준다.
이때, 원소들이 유일하지않다면 정렬될때 같은값이 붙어있으므로 그 영역의 넓이가 0이 되어 무시해도 되게 된다.
- 이 과정에서 Segment Tree를 사용해 구간갱신속도를 줄여 시간복잡도를 줄일수있다.
Input | Output |
첫 번째 줄에 사각형의 수 N이 입력된다. 2 ~ N + 1번째 줄에 차례대로 사각형의 왼쪽 아래점 X좌표, Y좌표, 높이, 너비가 주어진다 | 주어진 직사각형들의 그림자의 넓이를 구한다. |
import java.util.*;
public class Test {
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int ans = 0;
ArrayList<rect> d = new ArrayList<>();
ArrayList<Integer> x = new ArrayList<>();
ArrayList<Integer> y = new ArrayList<>();
for (int i = 0; i < n; i++) {
rect t = new rect();
t.x = scanner.nextInt();
t.y = scanner.nextInt();
t.width = scanner.nextInt();
t.height = scanner.nextInt();
d.add(t);
x.add(d.get(i).x);
x.add(d.get(i).x + d.get(i).width);
y.add(d.get(i).y);
y.add(d.get(i).y + d.get(i).height);
}
Collections.sort(x);
Collections.sort(y);
for (int i = 0; i < x.size() - 1; i++)
for (int j = 0; j < y.size() - 1; j++)
for (int k = 0; k < n; k++)
if ( x.get(i) >= d.get(k).x && x.get(i + 1) <= d.get(k).x + d.get(k).width &&
y.get(j) >= d.get(k).y && y.get(j + 1) <= d.get(k).y + d.get(k).height) {
ans += (x.get(i + 1) - x.get(i)) * (y.get(j + 1) - y.get(j));
break;
}
System.out.println(ans);
}
static class rect {
int x, y, width, height;
rect(){}
}
}
CCW (Counter Clock-Wise)
한 선과 한 점의 위치관계를 구할때 사용하는 알고리즘
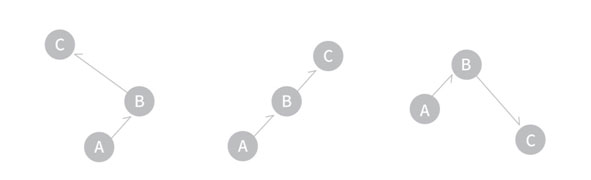
선분 AB와 점 C가 일직선상에 있는지, 반시계 방향에 있는지, 시계방향에 있는지 알려준다.
기하문제에 주로 사용되며, 이 알고리즘을 이용하는 알고리즘으로 대표적으로 Convex Hull이 있다.
구현
AB벡터와 BC벡터의 외적이 1. 음수값이면 시계방향 2. 0이면 일직선 3. 양수값이면 반시계방향에 있는것으로 판단한다. 두 벡터 {X1, X2}, {Y1, Y2}의 외적은 X1Y2 - X2Y1이다. 따라서 점 ABC가 A(X1,Y1), B(X2,Y2), C(X3,Y3)라면, CCW값은 (X2-X1)*(Y3-Y2)-(Y2-Y1)*(X3-X2)이다.

Input | Output |
첫 줄에 테스트케이스의 수 T가 주어집니다. 각 테스트케이스 첫 줄에 점 A,B,C의 x,y값이 주어집니다. {Ax Ay Bx By Cx Cy} | 각 테스트케이스마다 세 점의 관계를 출력합니다. 반시계방향이면 1 일직선상이면 0 시계방향이면 -1 |
import java.util.*;
public class Test {
public static class Point {
int x, y;
Point(int x, int y) {
this.x = x;
this.y = y;
}
};
public static int ccw(Point a, Point b, Point c) {
Point ab = new Point(b.x - a.x, b.y - a.y);
Point bc = new Point(c.x - b.x, c.y - b.y);
int ret = ab.x * bc.y - ab.y * bc.x;
if (ret > 0) return 1; //반시계 방향
else if (ret == 0) return 0; //일직선상
else return -1; //시계 방향
}
static int T;
public static void main(String args[]) {
Scanner scanner = new Scanner(System.in);
Point P[] = new Point[3];
T = scanner.nextInt();
for (int i = 0; i < T; i++) {
for (int j = 0; j < 3; j++) {
int x = scanner.nextInt();
int y = scanner.nextInt();
P[j] = new Point(x, y);
}
int result = ccw(P[0], P[1], P[2]);
System.out.println(String.valueOf(result));
}
}
}
Convex Hull 볼록 껍질
2차원 평면에 여러 점이 주어졌을때 모든 점을 포함하는 볼록껍질을 이루는 점들을 구하는 알고리즘
위의 CCW 알고리즘이 사용되며, Graham's scan 방법을 사용해 구현한다.
- 점들을 정렬하고, 가장 아래의 점 P0를 골라 스택에 push한다. (여러개라면 가장 왼쪽의 점)
- P0와 나머지 점들과의 기울기를 구해, x축과의 각도를 구한다.
- 각도를 기준으로 오름차순 정렬한다.
- P0와 각도가 작은 순으로 P1, P2, P3 ... Pk로 네이밍.
- 스택에 P1을 push한다.
- P0,P1,P2에 CCW를 적용해 양수값(반시계방향)이면 P2를 push, 0 or 음수값이면 pop한뒤 P2를 push한다.
- P1,P2,P3에 CCW를 적용해, 양수값(반시계방향)이면 P3를 push, 0 or 음수값이면 pop한뒤 P3를 push한다.
- 반복
- 마지막 정점 Pk까지 수행하면, 스택에 Convex Hull을 이루는 점들이 들어간다.
(코드에선 일단 pop한뒤, ccw값에 따라 양수면 pop한값 다시 push, 새로운값 push 하는 방식으로)

Input | Output |
| 볼록 껍질을 이루는 점의 개수를 출력합니다. |
아래 코드는 '각도기준 오름차순'위해 'cos값기준 내림차순'으로 정렬하였다.
import java.util.*;
class Point implements Comparable<Point> {
double x, y;
double scope;
Point(double x, double y) {
this.x = x;
this.y = y;
this.scope = 0;
}
public int compareTo(Point P) {
if (this.scope == P.scope) {
//각도 같은경우는 거의 일어나지않음
if (this.y == P.y) {
return (int) (this.x - P.x);
} else {
return (int) (this.y - P.y);
}
} else {
//return (int) (this.scope - P.scope);
/*그냥 int로 바로 casting하면 값손실 일어나서
별도로 분기문 만들어 return 해줌*/
if (this.scope - P.scope > 0)
return -1;
else if (this.scope - P.scope == 0)
return 0;
else
return 1;
}
}
}
public class Test {
static Point P[] = {new Point(6,0), new Point(14,1), new Point(16,6)
, new Point(14,8), new Point(12,10), new Point(13,6)
, new Point(7,8), new Point(7,11), new Point(3,7)
, new Point(0,3)};
public static int ccw(Point a, Point b, Point c) {
Point ab = new Point(b.x - a.x, b.y - a.y);
Point bc = new Point(c.x - b.x, c.y - b.y);
double ret = ab.x * bc.y - ab.y * bc.x;
if (ret > 0) return 1; //반시계 방향
else if (ret == 0) return 0; //일직선상
else return -1; //시계 방향
}
static int N;
static double getDistance(Point A, Point B) {
return Math.sqrt(Math.pow(A.x - B.x, 2.0) + Math.pow(A.y - B.y, 2.0));
}
static void setScope(Point P0) {
for (int i = 1; i < N; i++) {
P[i].scope = (P[i].x - P0.x) / getDistance(P0, P[i]); //cosin value
}
}
static void printPoints(Point[] P) {
for(Point var : P)
System.out.printf("(%d,%d,%.2f) ", (int)var.x, (int)var.y, var.scope);
System.out.println();
}
static Stack<Integer> ConvexHull() {
Arrays.sort(P);
printPoints(P);
setScope(P[0]);
Arrays.sort(P, 1, N);
printPoints(P);
Stack<Integer> convexhull = new Stack<>();
convexhull.push(0);
convexhull.push(1);
for (int i = 2; i < N; i++) {
while (convexhull.size() >= 2) { //ccw값이 양수면 바로 push, 0or음수면 pop하다가 양수나올때 push. 기본stack값인 0,1 나올때까진 계속함
int Last = convexhull.pop();
int pLast = convexhull.peek();
if (ccw(P[pLast], P[Last], P[i]) > 0) {
convexhull.push(Last);
break;
}
}
convexhull.push(i);
}
return convexhull;
}
public static void main(String args[]) {
N = P.length;
int result = ConvexHull().size();
System.out.println(String.valueOf(result));
}
}

'Algorithm' 카테고리의 다른 글
| 알고리즘) Graph - Network Flow, Bipartite Matching (0) | 2019.09.13 |
|---|---|
| 알고리즘) KMP (Knuth–Morris–Pratt, 문자열 탐색 알고리즘) (0) | 2019.09.13 |
| 알고리즘) Permutation, Combination (순열, 조합) (0) | 2019.09.13 |
| 알고리즘) 5 DP Examples - Knapsack, LCS, LIS, Edit Distance, Matrix Chain Multiplication (0) | 2019.09.13 |
| 알고리즘) DP (Dynamic Programming, 동적계획법), ex: Coin Change Problem (0) | 2019.09.13 |
- Total
- Today
- Yesterday
- OneToMany
- socket
- 회고
- Algorithm
- Java
- reversing
- mysql
- queue
- Stack
- 해외여행
- 프로그래머스
- javascript
- Android Studio
- JPA
- C
- 리버싱
- FRAGMENT
- graph
- 개발자
- bfs
- git
- brute-force
- dfs
- 우아한 테크코스
- Data Structure
- sort
- 웹해킹
- Android
- Vo
- webhacking.kr
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
