티스토리 뷰
Sieve of of Eratosthenes (에라토스테네스의 체)
소수판별 알고리즘
필요한 범위의 배열 생성후, 2부터 시작해서 차례대로 배수들을 소수가 아닌것으로 체크

최적화
첫번째 반복문의 범위를 1-N이 아닌 1-sqrt(N)으로 바꿔 속도 향상 가능.

A의 약수를 구할때 1-sqrt(A)까지만 구하면 되는것은 자명하다.
해당범위내에서 N번째 소수를 구하는 경우라면, 1-N까지 모두 돌려야하겠지만
해당범위내에서 특정숫자 N이 소수인지 판별하는 경우라면, 1-sqrt(N)으로 최적화 가능.
import java.lang.Math;
import java.util.Scanner;;
public class Test {
private final static int MAX = 50;
static boolean isPrime[] = new boolean[MAX+1];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
for(int i=2; i<=MAX; i++) {
isPrime[i] = true;
}
for(int i=2; i<=Math.sqrt(MAX); i++) {
if(isPrime[i] == false)
continue;
for(int k=i+i; k<=MAX; k+=i) {
isPrime[k] = false;
}
}
int testcase = scanner.nextInt();
for(int i=0; i<testcase; i++) {
int n = scanner.nextInt();
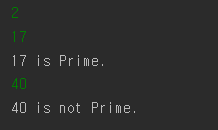
if(isPrime[n])
System.out.println(n+" is Prime.");
else
System.out.println(n+" is not Prime.");
}
}
}
'Algorithm' 카테고리의 다른 글
| 알고리즘) Shell/Radix Sort (셸/기수 정렬) (0) | 2019.09.12 |
|---|---|
| 알고리즘) Quick/Merge Sort (퀵/병합 정렬) (0) | 2019.09.12 |
| 알고리즘) Selection/Insertion/Bubble Sort (선택/삽입/버블 정렬) (0) | 2019.09.12 |
| 알고리즘) Linear/Binary Search (선형/이진 검색) (0) | 2019.09.12 |
| 알고리즘) Fibonacci (피보나치) (0) | 2019.09.12 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
TAG
- OneToMany
- javascript
- webhacking.kr
- 웹해킹
- bfs
- 회고
- FRAGMENT
- 우아한 테크코스
- 해외여행
- queue
- Vo
- dfs
- sort
- C
- socket
- mysql
- Data Structure
- 개발자
- 프로그래머스
- reversing
- Java
- Algorithm
- git
- JPA
- Android
- brute-force
- graph
- 리버싱
- Android Studio
- Stack
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
글 보관함
